Overview
Last time we created a model, now it’s time to put it use. Our goal this time will be to render a sphere onto the screen.
UV Sphere
The kind of sphere we’ll be generating is called a UV sphere. There are other, more visually appealing ways to build a sphere, but for our purposes a UV spehere will do. See here for a discussion of UV spheres vs icospheres
A UV sphere is built by evaluating the parametric equation for a sphere on a grid. Since our model matrix will handle moving the sphere from local coorindates to world coordinates we can without loss of generality place the sphere at the origin of it’s local coordinate system.
A sphere can be parameterized by 3 coordinates (r,u,v). We’ll be dealing with a hallow sphere so the radius, r, will be fixed. u can range from [0,2pi] and v can range from [0,pi]. You can think of u and v as longitude and latitude.
To translate back into cartesian coordinates we make use of the following tranformation rules.
x = rcos(u)sin(v)
y = rcos(v)sin(u)
z = rsin(u)sinv(v)
So in order to generate a sphereical mesh we will evaluate the parametric equation on a rectangular uv grid, and then translate these points into cartesian coordinates
Here’s what that looks like in C++
void Sphere::UVSphereMesh(const GLfloat radius, const GLuint numU, const GLuint numV, Mesh& mesh)
{
GLfloat uStart = 0.0f;
GLfloat vStart = 0.0f;
GLfloat uEnd = 2*M_PI;
GLfloat vEnd = M_PI;
GLfloat uStep = (uEnd - uStart)/numU;
GLfloat vStep = (vEnd - vStart)/numV;
List3df vertices(numU*numV*4,3);
List3di faces(numU*numV*2,3);
int vIndex = -1;
int fIndex = -1;
int eIndex = 0;
for(int i = 0; i < numU; i++)
{
GLfloat u = uStart + i*uStep;
GLfloat un = (i+1 == numU) ? uEnd : (u + uStep);
for(int j = 0; j < numV; j++)
{
GLfloat v = vStart + j*vStep;
GLfloat vn = (j+1 == numV) ? vEnd : (v + vStep);
Vector3Gf p0 = radius*Vector3Gf(cos(u)*sin(v),cos(v),sin(u)*sin(v));
Vector3Gf p1 = radius*Vector3Gf(cos(u)*sin(vn),cos(vn),sin(u)*sin(vn));
Vector3Gf p2 = radius*Vector3Gf(cos(un)*sin(v),cos(v),sin(un)*sin(v));
Vector3Gf p3 = radius*Vector3Gf(cos(un)*sin(vn),cos(vn),sin(un)*sin(vn));
vertices.row(++vIndex) = p0;
vertices.row(++vIndex) = p1;
vertices.row(++vIndex) = p2;
vertices.row(++vIndex) = p3;
fIndex++;
faces(fIndex,0) = eIndex+0;
faces(fIndex,1) = eIndex+2;
faces(fIndex,2) = eIndex+1;
fIndex++;
faces(fIndex,0) = eIndex+2;
faces(fIndex,1) = eIndex+3;
faces(fIndex,2) = eIndex+1;
eIndex += 4;
}
}
mesh = Mesh(vertices,faces);
};
Each inner loop creates 2 triangles like so
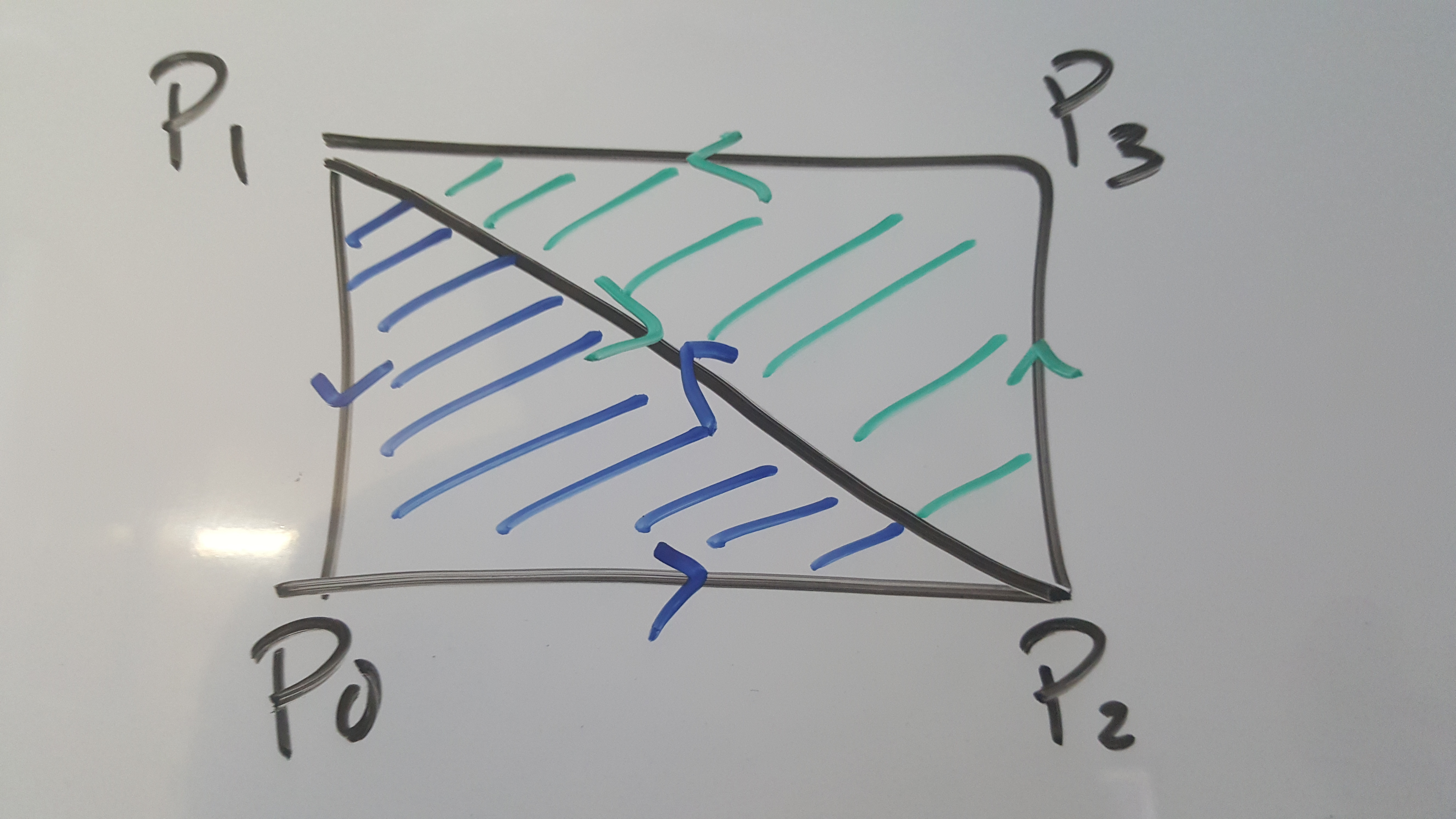
That’s the meat of the Sphere class right there. The rest is just trimmings.
Sphere
#include<mesh.h>
#include <GL/glew.h>
#include <Eigen/Core>
#include <vector3G.h>
#include <physics_entity.h>
#include <model.h>
#ifndef SPHERE
#define SPHERE
/**
\brief A sphere
A Sphere is defined by a center and a radius. Sphere extends Model. As such is will be rendered to the screen
**/
class Sphere : public Model
{
private:
GLfloat m_radius;
Vector3Gf m_center;
void UVSphereMesh(const GLfloat radius, const GLuint numU, const GLuint numV, Mesh &mesh);
public:
/**
Constructs a Sphere of radius 1.0, mass 1.0, centered at the origin
**/
Sphere();
/**
Constructs a sphere
@param radius radius of the Sphere
@param position position of the Sphere (ie its center)
**/
Sphere(GLfloat radius, Vector3Gf position);
};
#endif
#include <sphere.h>
#include <iostream>
Sphere::Sphere() : Model()
{
m_radius = 1.0f;
m_center = Vector3Gf(0.0f,0.0f,0.0f);
UVSphereMesh(m_radius, 20, 20, m_mesh);
};
Sphere::Sphere(GLfloat radius, Vector3Gf position) : Model()
{
m_radius = radius;
m_center = position;
m_model_matrix.col(3) << position(0), position(1), position(2), 1.0f;
UVSphereMesh(m_radius, 20, 20, m_mesh); // model matrix handles translation of mesh so we use (0,0,0) as mesh center
};
void Sphere::UVSphereMesh(const GLfloat radius, const GLuint numU, const GLuint numV, Mesh& mesh)
{
GLfloat uStart = 0.0f;
GLfloat vStart = 0.0f;
GLfloat uEnd = 2*M_PI;
GLfloat vEnd = M_PI;
GLfloat uStep = (uEnd - uStart)/numU;
GLfloat vStep = (vEnd - vStart)/numV;
List3df vertices(numU*numV*4,3);
List3di faces(numU*numV*2,3);
int vIndex = -1;
int fIndex = -1;
int eIndex = 0;
for(int i = 0; i < numU; i++)
{
GLfloat u = uStart + i*uStep;
GLfloat un = (i+1 == numU) ? uEnd : (u + uStep);
for(int j = 0; j < numV; j++)
{
GLfloat v = vStart + j*vStep;
GLfloat vn = (j+1 == numV) ? vEnd : (v + vStep);
Vector3Gf p0 = radius*Vector3Gf(cos(u)*sin(v),cos(v),sin(u)*sin(v));
Vector3Gf p1 = radius*Vector3Gf(cos(u)*sin(vn),cos(vn),sin(u)*sin(vn));
Vector3Gf p2 = radius*Vector3Gf(cos(un)*sin(v),cos(v),sin(un)*sin(v));
Vector3Gf p3 = radius*Vector3Gf(cos(un)*sin(vn),cos(vn),sin(un)*sin(vn));
vertices.row(++vIndex) = p0;
vertices.row(++vIndex) = p1;
vertices.row(++vIndex) = p2;
vertices.row(++vIndex) = p3;
fIndex++;
faces(fIndex,0) = eIndex+0;
faces(fIndex,1) = eIndex+2;
faces(fIndex,2) = eIndex+1;
fIndex++;
faces(fIndex,0) = eIndex+2;
faces(fIndex,1) = eIndex+3;
faces(fIndex,2) = eIndex+1;
eIndex += 4;
}
}
mesh = Mesh(vertices,faces);
};
Rendering
Without going into details about how OpenGL renders a scene I’ll just state the render loop
Sphere sphere(1.0f, Vector3Gf(0.0f,0.0f,0.0f));
while(!glfwWindowShouldClose(window))
{
// Frame data to smooth out camera movement
GLfloat current_frame = glfwGetTime();
delta_time = current_frame - last_frame;
last_frame = current_frame;
glfwPollEvents();
DoMovement(); // Move cemera
// Switch between wireframe and filled rendering
if(keys[GLFW_KEY_F])
{
glPolygonMode( GL_FRONT_AND_BACK, GL_LINE );
}
if(keys[GLFW_KEY_G])
{
glPolygonMode( GL_FRONT_AND_BACK, GL_FILL );
}
glClear(GL_COLOR_BUFFER_BIT);
glEnable(GL_DEPTH_TEST);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
// Use our simple shader
shader.Use();
Eigen::Matrix<GLfloat,4,4> view;
view = camera.GetViewMatrix();
Eigen::Matrix<GLfloat,4,4> projection;
projection = perspective<GLfloat>(camera.m_zoom, ((GLfloat)WIDTH)/((GLfloat)HEIGHT), 0.1f, 100.0f);
GLint modelLoc = glGetUniformLocation(shader.Program, "model");
GLint viewLoc = glGetUniformLocation(shader.Program, "view");
GLint projectionLoc = glGetUniformLocation(shader.Program, "projection");
// Set view and projection matricies in shader
glUniformMatrix4fv(viewLoc, 1, GL_FALSE, view.data());
glUniformMatrix4fv(projectionLoc, 1, GL_FALSE, projection.data());
// Grab Vertex Array Object Id for sphere
GLuint VAO = sphere.GetMesh().GetVAO();
// Get model matrix for sphere and set it in shader
Eigen::Matrix<float,4,4> model_matrix = sphere.GetModelMatrix();
glUniformMatrix4fv(modelLoc, 1, GL_FALSE, model_matrix.data());
// Render sphere
glBindVertexArray(VAO);
glDrawElements(GL_TRIANGLES, 2*sphere.GetMesh().GetNumEdges(), GL_UNSIGNED_INT,0);
glBindVertexArray(0);
glfwSwapBuffers(window);
}
Results
Ta da! Just like I promised way back in the setup we’ve finally rendered something to the screen. We can learn a lot about physical simulation with just this simple sphere. As later articles will show.
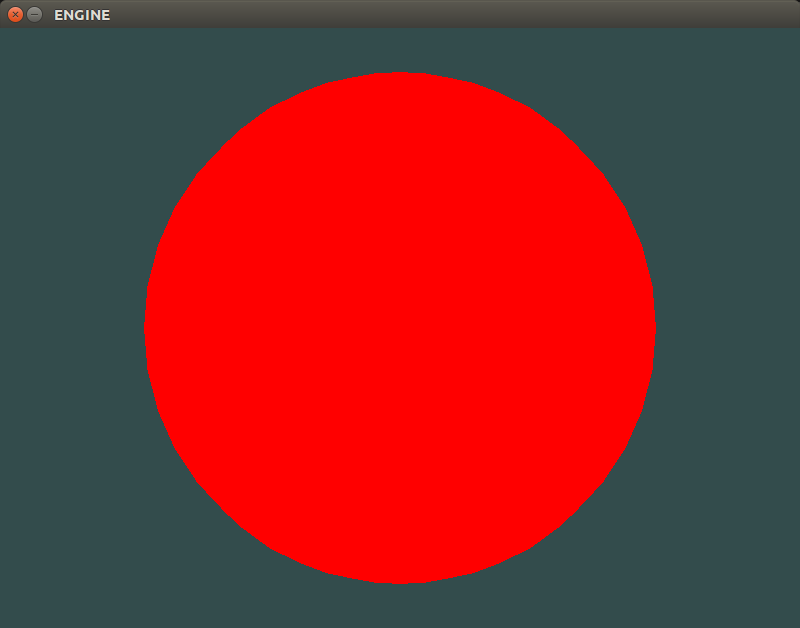
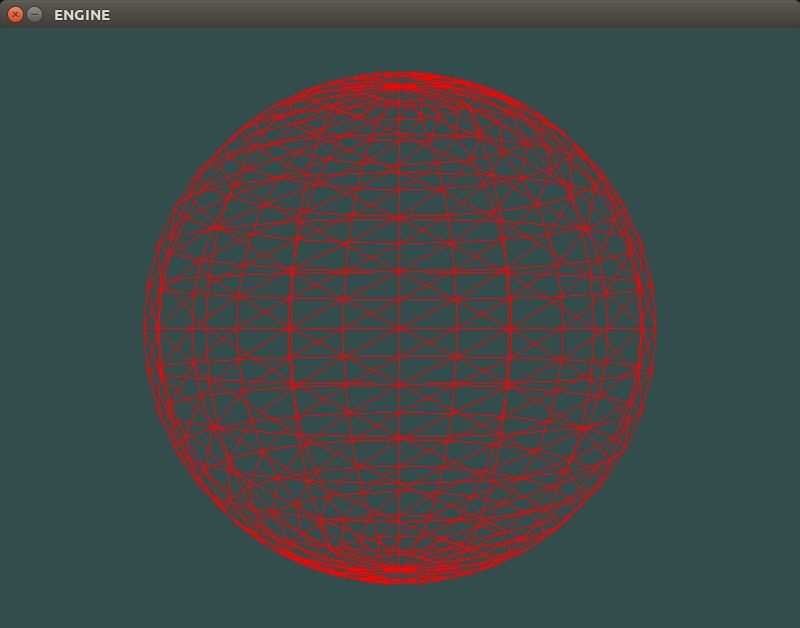
Full Code
For the full code you can clone this branch. You’ll want to look at sphere.h mesh.h model.h sphere.cpp mesh.cpp model.cpp and main.cpp