Rotations

Overview

In this article we’ll discuss what exactly is a rotation and how do we represent one in a computer.

Representing a rotation geometrically

First lets talk about what a rotation is. Geometrically a rotation is an axis specified by a normalized direction vector $\hat{u}$ and an angle $\theta$. We say that the rigid body is rotated about $\hat{u}$ by an angle $\theta$

Here I’ve draw the rotation axis as going through the center of the disk. However there is no reason that need be the case. $\vec{u}$ can be any arbitrary axis. The image shows a point on the surface of the disk $\vec{x}$ being rotated to it’s new position $\vec{x}'$.

One way to represent rotations algebraically is to use Euler angles. These are the familar pitch, yaw, and roll you may have heard referenced in aviation games or television shows. However these suffer from a problem known as gimbal lock. Insead we will be using objects known as quaternions.

Quaternions

It turns out that the nicest way to manipulate rotations algebraically is the quaternions $\mathbb{H}$. A quaternion is equivalent to a vector in $\mathbb{R}^{4}$ but for one crucial difference, $\mathbb{H}$ comes equiped with a product operation that makes it a division algebra. Meaning it is possible to multiply and divide quaternions.

The easiest way to represent a quaternion $\tilde{q} \in \mathbb{H}$ is by the pair $(r,\vec{v})$ where $r \in \mathbb{R}$ and $\vec{v} \in \mathbb{R}^{3}$. $r$ is said to be the “real” part of $\tilde{q}$, whereas $\vec{v}$ is the “imaginary” part. With this formalism in hand we will procced to define all the basic operations one might perform on quaternions.

Sum and difference

\[ \tilde{q}_{1} \pm \tilde{q}_{2} = (r_{1} \pm r_{2}, \vec{v}_{1} \pm \vec{v}_{2}) \]

Product

\[ \tilde{q}_{1}\tilde{q}_{2} = (r_{1}r_{2} - \vec{v}_{1} \cdot \vec{v}_{2}, r_{1}\vec{v}_{2} + r_{2}\vec{v}_{1} + \vec{v}_{1} \times \vec{v}_{2}) \] where $\cdot$ and $\times$ are the familar dot product and cross product from $\mathbb{R}^{3}$

Conjugate

Keeping with the interpretation of $\vec{v}$ as the imaginary part of $\tilde{q}$ we can define a complex conjugate which simply involves the negation of $\vec{v}$.

\[ \tilde{q}^{*} = (r,-\vec{v}) \]

Norm

Like vectors in $\mathbb{R}^{n}$ quaternions have a notion of length that is defined through a norm \[ ||\tilde{q}||^{2} = \tilde{q}\tilde{q}^{*} = r^{2} + ||\vec{v}||^{2} \]

Multiplicative inverse

Using the relationship between the conjugate and the norm we can define the inverse of a quaterion to be \[ \tilde{q}^{-1} = \frac{\tilde{q}^{*}}{||\tilde{q}||^{2}} \] Verify for yourself that $\tilde{q}\tilde{q}^{-1} = 1$

Representing a rotation using quaternions

So how do we use quaternions to compute rotations? We can represent a rotation given by an axis $\hat{u}$ and an angle $\theta$ as a quaternion by utilzing an extension of Euler’s formula \[ \tilde{q} = \left(\cos\left(\frac{\theta}{2}\right),\sin\left(\frac{\theta}{2}\right)\hat{u}\right) \]

Now, we can embed an arbitrary point $\vec{x} \in \mathbb{R}^{3}$ into $\mathbb{H}$ by creating a new quaterion $\tilde{x} = (0,\vec{x})$. Using this embedding the rotated quaternion $\tilde{x}^{\prime}$ can be calculated as \[ \tilde{x}^{\prime} = \tilde{q}\tilde{x}\tilde{q}^{-1} \]

We can extract $\vec{x}^{\prime}$ from $\tilde{x}^{\prime}$ by ignoring its real part (which will be $0$ anyways). For a proof of this statement see the wikipedia article. It involves multiplying everything out and some algebra tricks to put the result into form of the Rodrigues rotation formula.

Relationship between quaternions and rotation matrices

To convert a quaternion $\tilde{q}=(q_{r},q_{i},q_{j},q_{k})$ to a rotation matrix $R$ we make use of the following formula \[ R= \begin{bmatrix} 1-2s(q_{j}^{2}+q_{k}^{2}) & 2s(q_{i}q_{j} - q_{k}q_{r}) & 2s(q_{i}q_{k} + q_{j}q_{r}) \\ 2s(q_{i}q_{j} + q_{k}q_{r}) & 1 - 2s(q_{i}^{2} + q_{k}^{2}) & 2s(q_{j}q_{k} - q_{i}q_{r}) \\ 2s(q_{i}q_{k} - q_{j}q_{r}) & 2s(q_{j}q_{k} + q_{i}q_{r}) & 1-2s(q_{i}^{2} + q_{j}^{2}) \end{bmatrix} \] where $s = \frac{1}{||q||^{2}}$. This matrix R will form the top-left $3 \times 3$ block of our model matrix.

Implementation

The implementation of Quaternion is mostly an exercise in operator overloading. I won’t bother to inline the code but I encourage you to look it over: quaternion.h quaternion.cpp

The only other matter at hand is to modify PhysicsEntity to store an orientation in the form of a Quaternion instance. The concrete realizations of PhysicsEntity and Model can load the orientation into the model matrix like so

m_model_matrix.block(0,0,3,3) = m_orientation.toRotationMatrix();

This must be done in the constructors and in the OnUpdateFromBuffer methods

Results

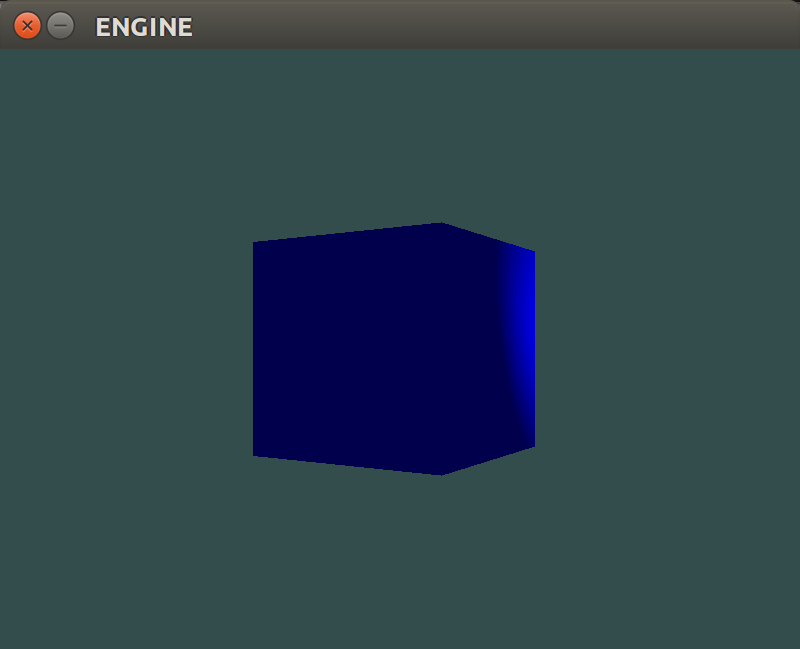
Here we’ve rotated the cube by $45$ degrees about the $y$ axis.

code